| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Tree/Binary_Tree
- Tree/Traversal
- CS/자료구조/Doubly_Linked_List
- tree
- CS/자료구조/Stack
- Tree/RBTree/Deletion
- Tree/BST
- 리버싱
- 코드엔진
- UTCTF
- Tree/RBTree
- CS/자료구조/Linked_List
- Tree/AVL/Deletion
- ctf
- CS/자료구조/Circular_Queue
- codeengn
- CS/자료구조/Circular_Linked_List
- Tree/RBTree/Insertion
- forensic
- Tree/AVL/Insertion
- reversing
- Tree/AVL
- Tree/Binary_Search_Tree
- CS/자료구조/Priority_Queue
- CS/자료구조/Singly_Linked_List
- CS/자료구조/Queue
- Today
- Total
SuperVingo
Self-balancinig BST 자가 균형 이진 탐색 트리 본문
Self-balancinig BST 자가 균형 이진 탐색 트리
SuperVingo 2024. 1. 4. 21:20여기에서는 AVL과 Red-Black Tree에 대해서 설명한다.
Self-balancing Binary Search Tree
"자가 균형 이진 탐색 트리(Self-balancing Binary Search Tree)"라고 한다.
이 트리는 트리의 전체적인 균형을 맞추는데, 이러한 과정이 필요한 이유는 BST의 Worst Case를 보아야한다.
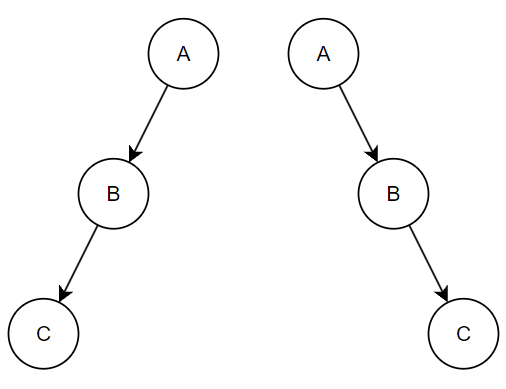
바로 편향 이진 트리 상황이다.

만약 N개의 노드가 있다면, 최대 트리의 높이는 logN이므로, 탐색 시간은
$$ O(log N) $$
이 된다.

하지만, 편향 이진 트리의 경우에는 만약 N개의 노드가 있다면, 최대 트리의 높이가 N이 되어
탐색시간은 $$ O(N) $$ 이 된다. 이러한 문제를 해결하는 것은 이진 트리의 양쪽 높이를 일정하게 유지하는 것이다.
이를 위해서 자가 균형 이진 탐색 트리가 등장하게 되었다.
AVL
Adelson-Velskii 와 Landis에 의해 1962년에 제안된 자가 균형 이진 탐색 트리로,
모든 노드의 왼쪽과 오른쪽 서브트리의 높이 차가 1인 이진탐색트리
즉, 양쪽 트리의 균형을 맞추는 게 목적이다.

균형 인수(Balance Factor) = 왼쪽 서브트리 높이 - 오른쪽 서브트리 높이
모든 노드의 균형인수를 $$ \pm1 $$로 맞춰진 이진탐색트리면 AVL이라고 한다.
만약 균형인수가 2 이상으로 차이가 생기면 리밸런싱 과정을 진행한다.
Insertion 과정은 일반 BST와 같지만, 삽입 후 균형인수를 체크하여 리밸런싱을 진행한다.
LL Type

LL Type은 왼쪽 자식의 왼쪽 서브트리에 삽입한 경우에 생기는 불균형이다.

이 경우에는 Rotation을 통해서 바로잡을 수 있다.

General Case는 다음과 같다.
RR Type

RR Type은 오른쪽 자식의 오른쪽 서브트리에 삽입한 경우에 생기는 불균형이다.

이 경우에도 LL Type과 비슷하게 Rotation을 통해서 해결한다.

LR Type

LR의 경우에는 LL Type으로 바꿀 수 있다. LL Type으로 바꾼 후, LL Type Rotation으로 해결한다.
RL Type

RL Type도 똑같이 RR Type으로 바꿀 수 있다. 바꾼 후 RR Type Rotation 진행.
Red-Black Tree

레드 블랙 트리의 경우에는 복잡하지만, 효율적이고, Worst Case에서도 충분히 좋은 성능을 보여주어 많이 사용되고 있다.
사진과 같이 노드는 Black / Red 두 개의 색깔을 가지고 있다.
레드 블랙 트리의 특징은
- 루트 노드는 Black Node이다.
- 모든 NIL(Null Leaf, 데이터는 없는 가상의 리프 노드)은 검은색이다.
- 빨간색 노드가 연속으로 나올 수 없다. 즉, 빨간색 노드의 자식은 모두 검은색이여야 한다.
- 모든 리프 노드까지 가는데 만나는 검은색 노드 수가 같다.
Insertion

삽입 과정은 다른 BST와 같이 삽입을 진행한다. 이때 삽입되는 노드는 Red Node이다.
이때 조심해야 할 상황은 다음과 같이 레드 노드가 연속으로 나오는 상황이다.
이때, 삼촌 노드의 색깔에 따라서 작업이 달라진다.
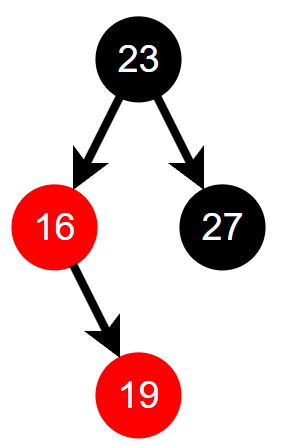
여기서 용어를 정리해보면
N : 새로 삽입한 노드, 노드 19
P : N의 부모 노드, 노드 16
G : P의 부모 노드, 노드 23
U : N의 삼촌 노드, 노드 27
Case 1 : U is Black Node / Restructing
만약, 삼촌 노드의 색깔이 검은색인 경우, Restructing 과정을 진행한다.
- N, P, G 노드를 정렬하여 가운데 값을 부모로 트리를 만든다.

- 새로운 부모 노드를 검은색 노드로 바꾸고, 자식은 빨간색 노드로 바꾼다.

그러면 다음과 같이 레드 노드가 2번 이어지지 않고, 정상적으로 트리가 형성되는 것을 확인할 수 있다.
Case 2 : U is Red Node / Recoloring
만약, 삼촌 노드의 색깔이 빨강인 경우에는 Recoloring 작업이 필요하다.

- P, U는 검은색 노드로, G는 빨간색 노드로 바꾼다.

- 이 때, G 노드를 빨강으로 바꾸면서 2가지 케이스가 생긴다.
- G 노드가 루트라면 다시 검은색으로 변경한다.
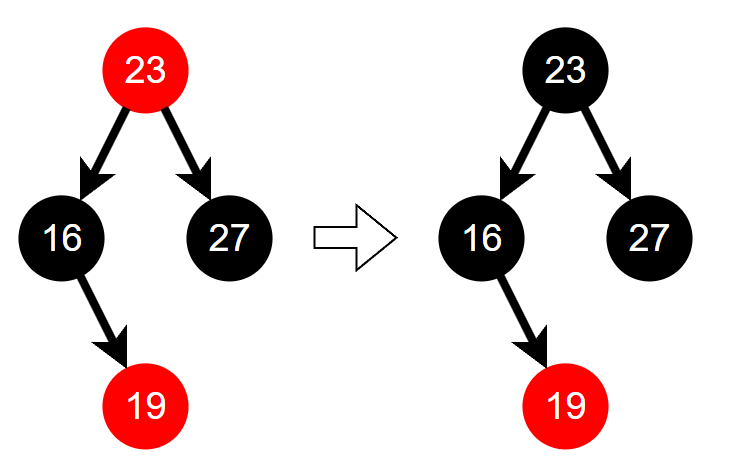
- G 노드를 바꾸면서 다시 빨강 노드가 연속된다면, 다시 Restructing 또는 Recoloring을 진행한다. !
- G 노드가 루트라면 다시 검은색으로 변경한다.

Deletion
노드를 삭제하는 경우에는
- 레드 노드 삭제
- 블랙 노드 삭제
두 가지 경우가 있다.
Case 1 : Delete Red Node
그냥 다른 연산 없이 BST 삭제 과정으로 삭제한다.
Case 2 : Delete Black Node
이 경우에는 검은색 노드를 지우게 되면,
4. 모든 리프 노드까지 가는데 만나는 검은색 노드 수가 같다.
라는 조건에 문제가 생길 수 있다.

이 경우에서는

다음과 같이 그냥 삭제하면 왼쪽까지 검은 노드 수가 바뀌게 되고,

그렇다고 부모를 검은색으로 올리면, 오른쪽으로 가는 검은 노드 수가 바뀌게 된다.
이를 위해서는 주변 상황에 따라서 다르게 처리해야 한다.
첫 번째로 형제의 노드의 색깔로 구분한다.
Case 2-1 : 이중 Black 노드의 형제 노드가 Red Node인 경우

노드 16을 제거 한다고 가정하면,
부모는 Red, 형제는 Black으로 바꾼 후, Rotation을 진행한다.
Case 2-2: 이중 Black 노드의 형제 노드가 Black인 경우
이 경우에는 주변 상황에 따라서 케이스가 또 나뉘게 된다.
이 때, 이중 Black 노드라는 개념이 등장하는데, Black 노드가 다시 Black 노드로 칠해지는 경우에
이중 Black 노드라고 한다.

이 글에서는 이중 블랙 노드를 회색으로 표시하겠다.
Case 2-2-1 : 이중 Black 노드의 형제, 형제 자식 모두 Black
- 삭제 후, 이중 블랙 노드의 형제는 Black, 부모는 Red로 칠한다.
- 이 과정을 이중 블랙 노드가 루트가 될 때까지 반복한다.

먼저 삭제를 진행한다. 그렇게 되면, NIL 노드가 올라면서 이중 블랙 노드가 된다.

이중 블랙 노드의 형제는 Black, 부모는 Red로 칠한다. 그러면 부모가 이중 블랙 노드가 된다.

이 과정을 반복해주면, 이중 블랙 노드가 루트가 되었다.

그러면 여기서 종료된다.
Case 2-2-2 : 이중 Black 노드의 형제가 Black, 형제 왼쪽 자식은 Red, 오른쪽 자식은 Black
이 경우에는
- 형제 노드를 Red, 형제 노드의 왼쪽 자식을 Black으로 칠한 후
- 형제 노드를 기준으로 Right Rotation을 한다.

7을 제거하면 노드 7위치에 NIL 노드가 들어오면서 이중 흑백 노드가 된다.

그리고 형제 노드는 Red, 형제 노드의 왼쪽 자식은 Black으로 칠한다.

그리고 Right Rotation을 한다.
Case 2-2-3 : 이중 Black 노드의 형제가 Black, 형제 자식 모두 Red
이 경우에는
- 부모 노드의 색을 형제에게 전달한다.
- 그리고 부모 노드와 형제 노드의 오른쪽 자식을 Black으로 칠한다.
- 부모 노드 기준으로 Left Rotation을 수행한다.
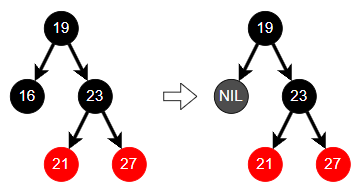
16을 제거한다고 가정한다. 그리고 부모 노드의 색을 형제에게 전달한다. 여기서는 검은색이므로 변화는 없다.
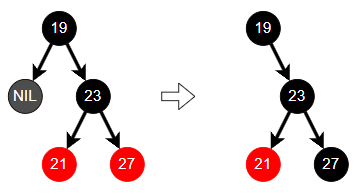
부모와 형제의 오른쪽 자식의 색을 Black으로 칠한다.

마지막으로 부모 노드 기준으로 Left Rotation을 진행한다.
'Computer Science[CS] > Data Structure[자료구조]' 카테고리의 다른 글
| Tree / BST (1) | 2024.01.03 |
|---|---|
| Stack, Queue (1) | 2024.01.01 |
| Doubly Linked List (0) | 2024.01.01 |
| Circular Linked List (0) | 2024.01.01 |
| Singly Linked List (0) | 2023.12.31 |




