| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Tree/AVL
- 코드엔진
- CS/자료구조/Doubly_Linked_List
- CS/자료구조/Circular_Queue
- CS/자료구조/Priority_Queue
- Tree/RBTree
- UTCTF
- Tree/Traversal
- ctf
- Tree/Binary_Tree
- Tree/AVL/Insertion
- CS/자료구조/Stack
- CS/자료구조/Singly_Linked_List
- codeengn
- forensic
- CS/자료구조/Queue
- reversing
- Tree/RBTree/Deletion
- CS/자료구조/Circular_Linked_List
- Tree/AVL/Deletion
- 리버싱
- Tree/Binary_Search_Tree
- tree
- Tree/BST
- CS/자료구조/Linked_List
- Tree/RBTree/Insertion
- Today
- Total
SuperVingo
Tree / BST 본문
Tree
Tree : 하나 이상의 Node로 이루어진 유한 집합.

| 용어 | 설명 |
|---|---|
| 루트(Root) 노드 | 부모가 없는 하나의 노드 / A 노드 |
| 차수(Degree) | 노드의 서브 트리 수 |
| 트리의 차수 | 각 노드의 차수 중 가장 큰 차수 |
| 단말(Leaf) 노드 | 차수 = 0인 노드 |
| 비단말 노드 | 차수 != 0인 노드 |
| 형제 | 부모가 같은 자식 |
| 노드 레벨 | 루트 노드 = 레벨 1부터 1씩 증가 |
| 트리의 높이 | 가장 깊은 노드의 레벨 |
Binary Tree

최대 차수가 2인 트리를 이진 트리, Binary Tree라고 함
왼쪽과 오른쪽 서브트리를 구분함.

즉, 두 트리는 다른 트리로 구분된다.
Skewed, Complete, Full

Skewed Binary Tree / 편향 이진 트리
오른쪽 또는 왼쪽 서브트리만 가짐

Complete Binary Tree / 완전 이진 트리
마지막 레벨을 제외하고 전부 채워져야하고, 마지막 레벨은 왼쪽부터 채워져야 함.
노드 $$ n $$개의 노드를 가진 완전 이진 트리의 높이 $$ \lceil{log_2(n+1)}\rceil $$

Full Binary Tree / 포화 이진 트리
완전 이진 트리와 다르게 마지막 레벨까지 모두 채워져있는 트리
깊이 $$ k $$면 노드 수는 $$ 2^k-1 $$
Traversal
트리에 있는 모든 노드를 방문하는 과정을 Tree Traversal, 트리 순회라고 한다.
In-Order Traversal
중위 순회라고도 불리며, 현재 노드를 방문하는 것이 중간에 진행되어 중위 순회이다.
- 왼쪽 서브트리로 이동
- 현재 노드 방문
- 오른쪽 서브트리로 이동
순서로 진행된다.
EX)

이 경우에는
D -> B -> G -> E -> H -> A -> C -> F
Pre-Order Traversal
전위 순회라고도 불리며, 현재 노드를 방문하는 것이 처음에 진행되어 전위 순회이다.
- 현재 노드 방문
- 왼쪽 서브트리로 이동
- 오른쪽 서브트리로 이동
순서로 진행된다.
EX)

이 경우에는
A -> B -> D -> E -> G -> H -> C -> F
Post-Order Traversal
후위 순회라고도 불리며, 현재 노드를 방문하는 것이 마지막에 진행되어 후위 순회이다.
- 왼쪽 서브트리로 이동
- 오른쪽 서브트리로 이동
- 현재 노드 방문
순서로 진행된다.
EX)

이 경우에는
D -> G -> H -> E -> B -> F -> C -> A
Level-Order Traversal
레벨 우선 순회라고도 불리며, 루트부터 같은 레벨에 있는 노드를 방문하는 순서로 진행된다.
EX)

이 경우에는
A -> B -> C -> D -> E -> F -> G -> H
Binary Search Tree (BST)

탐색을 효율적으로 하기 위한 트리 구조로,
- 이진 트리이고
- 모든 원소는 유일한 키를 가져야 하고
- 왼쪽 서브트리의 키 < 루트 키 < 오른쪽 서브트리의 키 형태여야 한다. 즉, 루트 키 기준으로 왼쪽은 루트 키보다 작은 숫자들이, 오른쪽에는 루트 키보다 큰 숫자들이 모이게 된다.
- 그리고 왼쪽 서브트리와 오른쪽 서브트리도 BST여야 한다.
Search

x = 탐색할 키 값
루트부터 시작해서
- 키 값 = x 면 탐색 성공
- 키 값 < x 면 오른쪽 서브트리로 이동
- 키 값 > x 면 왼쪽 서브트리로 이동
1~3번 과정을 반복하여 탐색을 진행한다.
Insertion

삽입의 경우에는 처음에 넣을려는 키 값을 탐색한다.
BST는 모든 원소들의 키 값은 유일해야하기 때문이다.
- 삽입하려는 키 값 탐색 시도
- 만약 탐색에 성공하면, 삽입은 실패한다.
- 만약 탐색에 실패하면, 실패한 자리에 삽입을 한다.
Deletion
삭제 과정에서도 먼저 탐색을 진행한다.
그 키 값이 존재해야 지울 수 있기 때문이다.
또한, BST에서 삭제를 한 후에도 BST 구조를 유지해야한다.
삭제할 노드의 차수 별로 Case가 존재한다.
- 삭제하려는 키 값 탐색 시도
- 만약 탐색에 성공하면, 노드의 차수를 고려하여 삭제
- 만약 탐색에 실패하면, 삭제 실패
Case #1
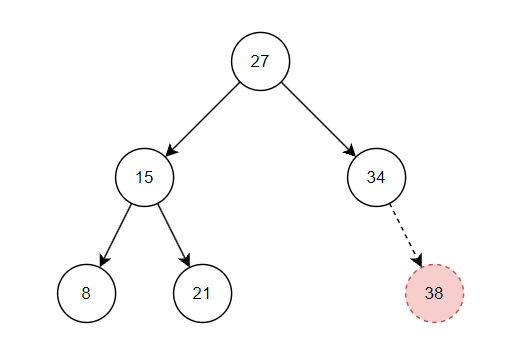
삭제할 노드의 차수가 0인 경우, 즉 단말 노드인 경우이다.
이 경우에는 부모 노드에서 자식 필드를 그냥 삭제하면 된다.
Case #2

삭제할 노드의 차수가 1인 경우이다.
이 경우에는 삭제될 노드의 자식을 부모에 연결하여 노드를 삭제한다.
Case #3

삭제할 노드의 차수가 2인 경우이다.
이 경우에는 삭제된 자리를 채울 후계자를 선정해야한다.
후계자는 총 2개의 후보가 있다.
- 왼쪽 서브트리에서 가장 큰 수
- 오른쪽 서브트리에서 가장 작은 값
1번의 경우에는 왼쪽 서브트리에서 오른쪽으로 쭉 진행하면 나오는 리프 노드고,
2번의 경우에는 오른쪽 서브트리에서 왼쪽으로 쭉 진행하면 나오는 리프 노드이다.

확인해보면 두 후계자 어느 쪽을 골라도 BST 구조가 유지되는 것을 볼 수 있다.
'Computer Science[CS] > Data Structure[자료구조]' 카테고리의 다른 글
| Self-balancinig BST 자가 균형 이진 탐색 트리 (0) | 2024.01.04 |
|---|---|
| Stack, Queue (1) | 2024.01.01 |
| Doubly Linked List (0) | 2024.01.01 |
| Circular Linked List (0) | 2024.01.01 |
| Singly Linked List (0) | 2023.12.31 |




